leetcode(리트코드)4-Meedian of Two Sorted Arrays

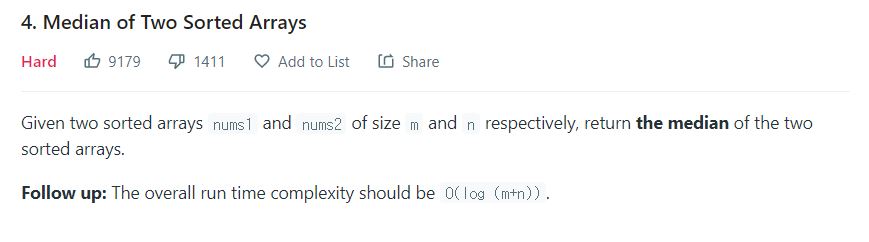
leetcode 4 - Median of Two Sorted Arrays 문제입니다.

1. 문제

https://leetcode.com/problems/median-of-two-sorted-arrays/

---

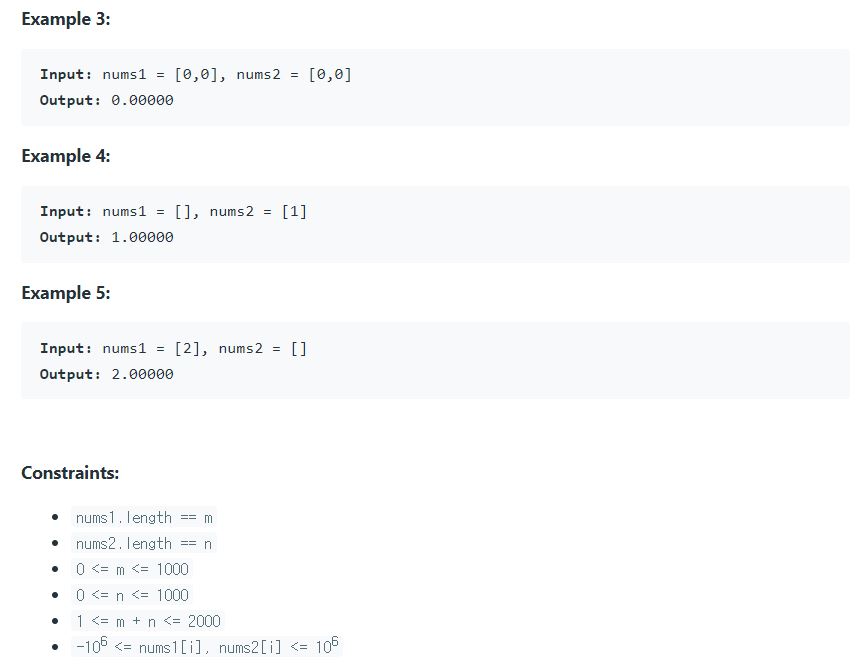
2. Input , Output

---

3. 분류 및 난이도

Hard 난이도 문제입니다.
leetcode Top 100 Liked의 문제입니다.

---

4. 문제 해석

• 이미 정렬된 2개의 배열을 Merge Sort를 합니다. Sort를한 결과의 mid값을 리턴합니다. 만약 배열의 크기가 짝수인 경우 mid-1까지 더해서 평균값을 리턴합니다.

---

5. code

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        //n과 m은 들어온 배열의 크기
        int n = nums1.size();
        int m = nums2.size();
        int mid = (n+m)/2;
        //check는 배열의 총 크기가 짝수인 경우, 홀수인 경우 판단을 위해 넣었습니다.
        bool check = (n+m)%2;
        double result = 0;
        vector<int> vec;
        int i = 0;
        int j = 0;
        //병합정렬
        while(i<n && j<m)
        {
            //mid+1까지만 정렬하면 됩ㄴ디ㅏ.
            if(vec.size()==mid+1)
                break;
            if(nums1[i] < nums2[j])
                vec.push_back(nums1[i++]);
            else
                vec.push_back(nums2[j++]);
        }
        int tmp = i > m ? j : i;
        while(i<n&& vec.size()!=mid+1)
        {
            vec.push_back(nums1[i++]);
        }
        while(j<m&&  vec.size()!=mid+1)
            vec.push_back(nums2[j++]);
        //만약 배열의 총 크기가 짝수면
        if(!check)
        {
            return (vec[mid] + vec[mid-1])/2.0;
        }
        return vec[mid];
    }
};

---

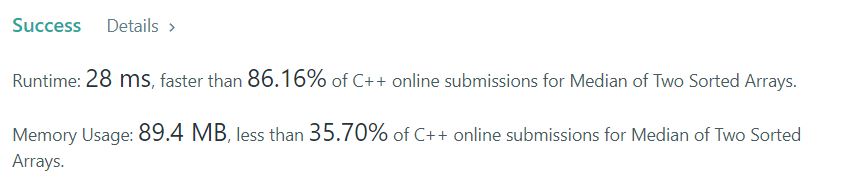
6. 결과 및 후기, 개선점

시간(86%)

시간이 빠른 코드(12ms) 99%

class Solution {
public:
    double findMedianSortedArrays(vector<int>& a1, vector<int>& a2) {
        int n1 = a1.size(), n2 = a2.size();
        if(n1 == 0 && n2 == 0)
            return 0;
        vector<int> v(n1+n2);
        int i1=0,i2=0,k=0;
        while(i1<n1 && i2<n2){
            if(a1[i1] < a2[i2]){
                v[k++] =  a1[i1++];
            }
            else{
                v[k++] =  a2[i2++];
            }
        }
        while(i1<n1){
            v[k++] =  a1[i1++];
        }
        while(i2<n2){
            v[k++] =  a2[i2++];
        }
        if((n1+n2) %2 == 0){
            int i = (n1+n2)/2,
            j = (n1+n2)/2 -1;
            return (v[i] + v[j])/2.0;
        }
        else{
            return v[(n1+n2)/2];
        }
    }
};

로직은 저와 똑같고 저와달리 배열의 끝까지 합병한다는 점에서 시간이 더 들거라 생각했습니다.