Baekjoon2004-조합 0의 개수

백준 사이트 2004 - 조합 0의 개수 문제입니다.

---

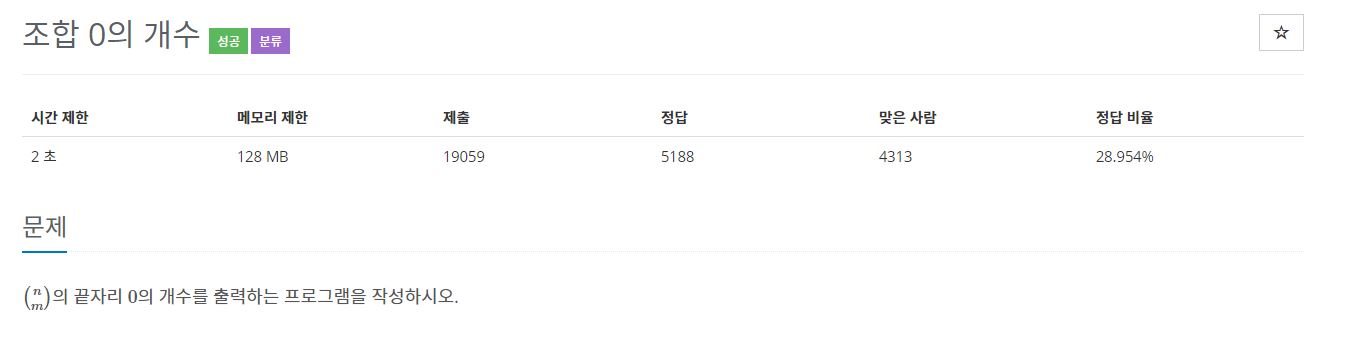
1. 문제

https://www.acmicpc.net/problem/2004

---

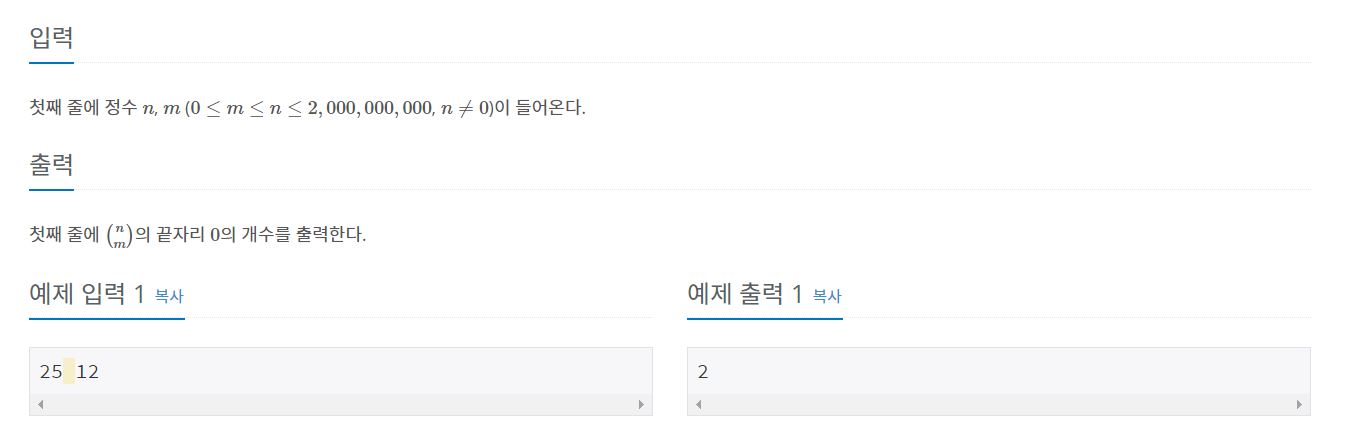
2. Input , Output

---

3. 분류 및 난이도

수학으로 분류되어 있는 문제입니다.
수의 범위가 굉장히 크고 일반적인 탐색으로는 당연히 시간초과가 날 것입니다. ex) n이 2억이고 m이 1억일 때 등.. 백준에서는 Sliver2의 난이도를 책정하고 있습니다.

---

4. 생각한 것들

• 10거듭제곱을 찾아야하는 문제입니다. 때문에 2의 배수와 5의배수 개수를 세줘야합니다.
  1. n-m만큼 반복문을 돌면서 2의 배수와 5의 배수만 찾아주기로 했습니다.
     -> 시간초과
  2. 문득 일반적인 상황에서는 2의 갯수가 5의 갯수가 많다고 생각했습니다. 당장 1~5범위만해도 5의 배수는 1개 2의 배수는 2,4로 2개라서 그렇습니다. 그래서 5의 갯수가 곧 10거듭제곱 수라 생각했습니다.
     -> ex) n = 125, m = 1인 경우 5의 갯수 3개 이지만 거듭제곱수는 3이아닌 0이다. 따라서 2의 거듭제곱도 세줘야함.
  3. 메모제이션 방법으로 배열에 먼저 5의 배수와 2의 배수를 넣고 꺼내는 방법을 생각했습니다.
     -> n = 300, m = 200인 경우 걸치는 경우가 있다. 256을 넘어가면서 2의 거듭제곱 갯수가 달라진다는 것. 경계선을 어떻게 해결할 지 생각했습니다.
  4. 위의 방식은 너무 복잡하고 어렵다는 것을 인지하고 다른사람들의 코드를 참고하여 따로 분리하는게 낫다고 생각함.
     -> ex) n! 따로 (n-m)! 따로 m! 따로 계산해줘야함. 세 식의 5의갯수 2의 갯수를 구해줘야함.

---

5. code

#include<iostream>
#include<algorithm>
#include<cmath>

using namespace std;

long long divide5(long long num)
{
	long long append = 0;
	for (long long i = 5; i <= num; i *= 5)
	{
		append += num / i;
	}
	return append;
}
long long divide2(long long num)
{
	long long append = 0;
	for (long long i = 2; i <= num; i *= 2)
	{
		append += num / i;
	}
	return append;
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
	long long n, m;
	cin >> n >> m;
	
	cout << min(divide5(n) - (divide5(n - m) + divide5(m)), divide2(n) - (divide2(n - m) + divide2(m)));
	

	return 0;
}

---

6. 후기

따지고보면 너무 당연한데, 이 방법을 생각하는데 너무 오랜 시간이 걸렸다.
문제 가지고 1시간 정도 고민을 해버려서 뇌가 녹아버렸다. 그래서 풀이를 참고하였지만, 유도하는데에 집중했다면 풀 지 않았을까.. 아쉬웠다.